We can see above, in the table, the dimensions of some physical quantities :
In the first line we find the different exponents of  L, which are Lo, L1 , L2 , L3 , L4, L5, L6
In the first column to the left we can see the negative exponents of  T, which are T0, T -1 , T -2 , T -3 , T -4 , T -5

• Distance or length (L dimension) in L1T0
• Surface (dimension L²) in L2 T0
• Volume (dimension L³) in L3 T0
• Velocity (dimension L / T) in L1 T - 1
• Acceleration (dimension L / T ²) in L1 T - 2
• Frequency (dimension 1 / T) in L0 T - 1
  

We also have:

• The square of frequency (dimension 1 / T ²) in L0 T - 2
• Flow = volume per second (dimension L³ / T) in L³ T - 1
  

Mass = L³ / T²

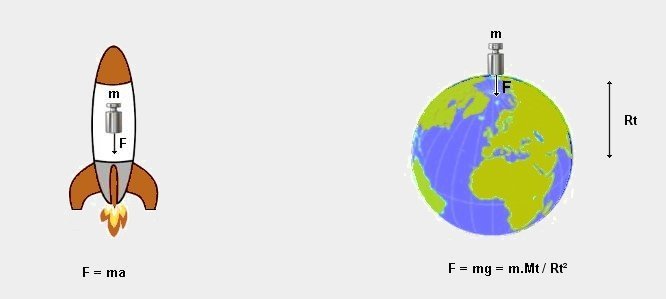
,A unitary mass m subject, in space, to an acceleration of 9,81 m/s (inside a rocket, for example) undergoes the same F force that it would undergo when it is subject to the earth's attraction.

Those two forces are of the same nature (in principle identical, nothing can distinguish them from each other), therefore they should have the same dimensions. Consequently, here we consider inertial mass and gravitational mass to be the exact same.

F = ma  with dimensions M . L / T²               (1)
F = K.m.Mt / Rt² with dimensions M² / L²       (2)

With Mt being the earth's mass (of dimension M) and Rt the earth's radius (of dimension L)
Comparing (1) and (2)'s dimensions we have M . L / T² = M² / L²

Therefore the dimensions of mass will be M = L³ / T² ( see appendix 1 )
From that we can express the mass in kg or as m³ / s² (see appendix 2 )

In (2) the Newton constant K is considered simply as a number without any dimension.

Some other measurable quantities:

• Momentum (mass . velocity) in L4 T -3
• Force (mass . acceleration) in L4 T -4
• Work or energy (force . displacement) in L5 T -4
• Power (energy/time) in L5 T -5
• Potential (energy/mass) or (mass/distance) in L2 T -2

We also have:

• Pressure (force/surface) in L2 T -4
• Stiffness of a spring (force/displacement) in L3T -4
• The square of mass (mass . mass) in L6 T -4
• The square of velocity (velocity . velocity) in L2 T -2
• The square of frequency (frequency . frequency) in T -2
• Action (energy . time) in L5 T -3
  

Some fundamental relations in physics

M.a = F          ( L3 T -2 )( L1 T -2 )   =   ( L4 T -4 )     =>     mass . acceleration = force
M.v = p          ( L3 T -2 )( L1 T -1 )   =   ( L4 T -3 )     =>     mass . velocity = momentum
M.v² = E        ( L3 T -2 )( L2 T -2 )   =   ( L5 T -4 )     =>     mass . (velocity)² = energy
M/R² = a       ( L3 T -2 )( L-2 )   =   ( L1 T -2 )            =>      mass / (distance )² = acceleration ( g = Mt / R²
M²/R = E      ( L3 T -2 )² (L-1)  =  ( L5 T -4 )              =>     (mass)² / (distance) = energy
M²/R² = F    ( L3 T -2 )² (L-2)  =  ( L4 T -4 )              =>     (mass)² / (distance)² = force
F.L = E           ( L4 T -4 )( L )  =  ( L5 T -4 )                   =>     force . distance = energy (work)
F / L = k        ( L4 T -4 )( L-1 )  =  ( L3 T -4 )                =>     force / distance = stiffness (of a spring, for example)
k / M = T -2  ( L3 T -4 )( L-3 T 2 ) = ( L0 T -2 )          =>     stiffness / mass = square of frequency
F . v = W        ( L4 T -4 )( L1 T -1 )  =  ( L5 T -5 )         =>     force . velocity = power
p / T = F        ( L4 T -3 )( L0 T -1 )  =  ( L4 T -4 )         =>     momentum / time = force