massa dimensão mass dimension masse dimension mass dimension massa dimensão mass dimension mass dimension masse dimension mass dimension massa massa dimensão mass dimension masse dimension mass dimension masse mass massa

Ao escrever as fórmulas de atração de duas massas M ( lei de Newton ) e de duas cargas Q ( força de Coulomb ) são duas forças de sinais opostos ( atração e repulsão).

      QQ/R²   =     ( -1 )   MM/R²                  (1)

        QQ       =     ( i ² )    MM                        (2)

De cada lado de (1) nós temos uma "Força". Estas forças deveriam, de acordo com nossa hipótese inicial, ter as mesmas "dimensões"

A força será chamada " negativa" no caso da atração ( duas massas que se atraem segundo Newton ) e " positiva", (caso de duas cargas elétricas de mesmo sinal que se repelem segundo a fórmula de Coulomb ).

A equação (2) dá duas soluções para Q ==>> Q = i M et Q = - i M com ( i)² = - 1
Nós teremos assim dois tipos de cargas elétricas tendo como dimensões : i M   e   - i M , ou ainda  i L³/T²   e   - i L³/T²
Estes dois tipos de cargas serão chamadas " carga positiva " e " carga negativa ".

Veremos imediatamente que duas cargas de mesmo sentido se repelem (força positiva) e duas cargas de sentidos opostos terão a tendência de se aproximar ( força negativa).

Da mesma forma duas massas positivas ou negativas terão tendência a se aproximar ( força negativa ) ao passo que duas massas de sinais contrários terão tendência a se afastar uma da outra ( força positiva ) segundo a mesma fórmula de Newton ( em 1/ R² )

As dimensões da carga serão assim as mesmas que as dimensões da massa, porém, serão complexas i L³/T² ou - i L³/T² certas grandezas elétricas também terão dimensões " complexas " i é um número dito " complexo " ou " imaginário " definido pela relação: ( i)² = - 1

Poderemos mesmo supor que uma deformação " espaço - tempo " terá uma parte real ( massa ) e uma parte complexa ( carga ) De modo geral M + iQ e a fórmula geral de atração das " massas - cargas " passa a ser:

F = ((M1+iQ1).(M2+iQ2))/R²       (3)

Esta força terá dois componentes reais ( duas massas se atraem e duas cargas de mesmo sinal se repelem)

((M1).(M2))/R²   e  ((iQ1).(iQ2))/R²  


Esta mesma força terá dois componentes complexos (uma carga une charge não tendo efeito sobre uma massa).

((M1).(iQ2))/R²   e   ((M2).(iQ1))/R²

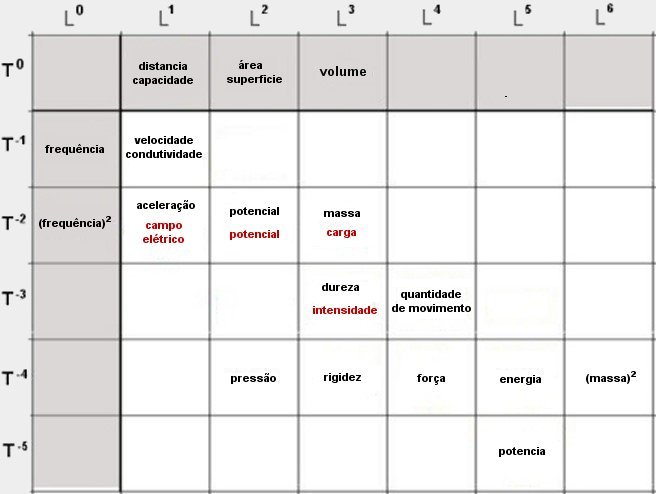
Grandezas complexas em vermelho

Sabendo que a carga elétrica tem como dimensões i L3 T -2 podemos determinar as dimensões de:

• " A intensidade I (ampere) = coulomb / segundo ou seja i L3 T -2 / T = i. L3 T -3
• " O potencial ( volt ) = coulomb / metro ou seja i L3 T -2 / L = . i L2 T -2
• " O campo elétrico = volt / metro ou seja i L2 T -2 / L = . i L T -2

Estas mesmas grandezas podem variar em relação ao tempo:

• " Variação da intensidade em relação ao tempo, ou seja i L3 T -3 / T = i L3 T -4
• " Variação de potencial em relação ao tempo, ou seja i L2 T -2 / T = i L2 T -3
• " Variação do campo elétrico em relação ao tempo, ou seja i L T -2 / T = i L T -3

As grandezas elétricas ( carga, potencial, intensidade, campo elétrico) seriam portanto grandezas complexas contrariamente às grandezas mecânicas que seriam reais e assim diretamente mensuráveis.

Para medir uma grandez elétrica ( carga, potencial, intensidade, campo elétrico) será necessário utilizar a eletricidade para obter uma grandeza real mensurável ( força ou deslocamento por exemplo).

Uma carga elétrica dará uma força (mensurável diretamente) ao interagir com uma outra carga ou com um campo elétrico.
Ao combinar duas grandezas complexas (i x i = i² = -1) volta-se ao real mensurável.

Uma carga (grandeza complexa), por exemplo, situada num campo elétrico (outra grandeza complexa) resultará numa força (grandeza real) que terá as mesmas dimensões que uma força mecânica ( L4 T -4 ).

Também podemos ver que um potencial elétrico (volt V) com uma intensidade (ampere A ) dará uma potência ( W = VA ) que terá as mesmas dimensões que uma potência mecânica ( L5 T -5 ).

Por outro lado uma carga (grandeza complexa) situada num campo gravitacional (grandeza real) resultará em uma grandeza real não mensurável (força complexa ?).

Algumas relações fundamentais em física (as grandezas complexas em vermelho, vamos escrever " L3 T -2 "  para  " i L3 T-2"  )

Q.Ê = F      ( L3 T -2 ) ( L1 T -2 )   =   ( L4 T -4 )    =>    carga . campo eletrico = força
Q.V= E      ( L3 T -2 ) ( L² T -2 )   =   ( L5 T -4 )    =>    carga . potencial = energia
Q / R = V    ( L3 T -2 ) ( L -1)  =   ( L2 T -2 )    =>    carga / distância = potencial
Q / R² = Ê    ( L3 T -2 ) ( L-2 )  =  ( L1 T -2 )    =>    carga / (distância)² = campo eletrico
Q² / R = E     ( L3 T -2 )² / (L-1)  =  ( L5 T -4 )    =>    (carga)² / distância = (carga)² / capacidade = energia
Q² / R² = F    ( L3 T -2 )² / ( L-2 ) =  ( L4 T -4 )    =>    (carga)² / (distância)² = força
V.I = W        ( L2 T -2 ) ( L3 T -3 )  =  ( L5 T -5 )    =>    potencial . intensidade = potência
I / V = 1 / R   ( L3 T -3 ) ( L-2 T 2 )  = ( L1 T -1 )    =>    intensidade / potencial = conductancia = 1/ résistancia
V.V = F         ( L2 T -2 ) ( L2 T- 2 ) = ( L4 T -4  ) =>    potencial . potencial = força
( I /T ) S = V   ( L3 T-4 ) ( L-1 T 2 ) = ( L2 T -2 )    =>    (variação de intensidade).( Coef self-induct ) = potencial
C V = Q       ( L1 T 0 ) ( L2 T -2 ) = ( L3 T -2 )    =>    capacidade . potencial = carga
I² . R = W     ( L3 T -3 )² (L-1 T 1) = ( L5 T -5 )    =>    (intensidade)² . (resistencia ) = potência

Dimensões de algumas grandezas em física ( as grandezas complexas estão em vermelho)

aceleração = ( L1 T -2 )
capacidade= ( L1 T 0 ) = espaço ou distância
campo eletrico( L1 T -2 ) ( Volts / mêtro )
campo gravífico ( L1 T -2 )
carga ( L3 T -2 ) ( Coulomb )
conductancia ( L1 T -1 )  =  1 / resistencia  ( velocidade )
dureza( L3 T -3 )
energia ( L5 T -4 ) = trabalho ( Joule )
força ( L4 T -4 ) ( Newton )
inductance ( L-1 T 2 ) = 1 / aceleração   ( Henry )
intensidade( L3 T -3 ) ( Ampère )
impulsão ( L4 T -3 ) ( quantidade de movimento )
massa ( L3 T -2 )
potencial eletrico ( L2 T -2 ) ( Volt )
potencial gravífico ( L2 T -2 )
pressão ( L2 T -4 ) ( Bar )
potencia ( L5 T -5 ) ( Watts )
resistencia ( L-1 T 1 ) = 1 / velocidade
rigidez( L3 T -4 )
velocidade ( L1 T -1 )