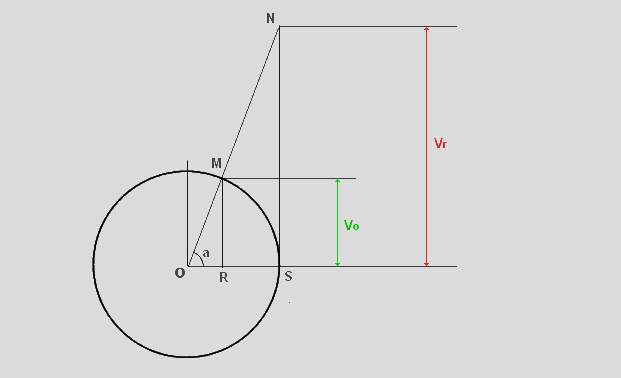
On peut représenter par un graphique très simple le rapport entre une vitesse observée ( qui bien sûr ne dépassera jamais la valeur de "1" soit la vitesse de la lumière ) et la vitesse dite " propre " qui sera celle réellement ressentie* par un voyageur dans l'espace. Nous appellerons cette vitesse " vitesse réelle " par opposition à la " vitesse observée "

Soit une circonférence de rayon unitaire ( O - S )

Pour n'importe quelle vitesse observée Vo ( inférieure à 1 = vitesse de la lumière ) on pourra définir un angle "a" tel que

Vo  =  sin (a)  =  M-R        ou encore        a  =  arc sin(Vo)

On sait que Vr ( vitesse propre ) vaut Vo / ( 1- Vo² )¹/²   =   Vo / cos (a)  =   sin (a) / cos (a)   =   tg (a) =   S - N

On aura donc :

Vo  =  sin (arc tg(Vr))   =   sin (a) 

Vr  =  tg (arc sin(Vo))  =   tg (a) 

Vr  =   Vo / cos (a)

Un photon :qui se déplace à une vitesse infinie pour lui même ( en effet, de son point de vue, il traverse l'univers instantanément, en " zéro " secondes ) mais il sera observé, se déplaçant à la vitesse de la lumière

Pour un voyageur de l'espace, sa vitesse Vr  ( vitesse ressentie *   mesurée par lui même )  sera perçue plus petite par un observateur fixe suivant la formule

Vo  =  sin (arc tg(Vr))       (  Vo représentant la vitesse observée dans un référentiel fixe  )

Et bien sûr  Vo ne dépassera jamais la valeur 1 qui est la vitesse de la lumière

Il semble donc plus correct de dire " une vitesse observée sera toujours inférieure à la vitesse de la lumière " au lieu de dire " on ne peut jamais dépasser le vitesse de la lumière "

* On .entend par " vitesse ressentie " la vitesse mesurée par le voyageur. En effet celui-ci peut mesurer à chaque instant son accélération et donc ( en intégrant par rapport à son temps ) sa vitesse par rapport à un observateur resté immobile

On pourra comparer aussi la masse réelle Mr ( masse propre ) .avec la masse observée Mo avec la relation

Mr   =   Mo . cos (a)     ( la masse observée sera toujours plus grande ) et nous aurons aussi :

Mr . Vr  =    Mo  . Vo  =   Pr   =  Po    Les quantités de mouvement ( observée et réelle ) sont égales.