dV/dT = ( 4 pi R² ) ( dR/dT ) ( surface de la sphère . variation du rayon )
ou bien   dR/dT = dV/dT / ( 4 pi R² )

Un point situé sur la sphère va se rapprocher du centre de celle-ci a une vitesse de dR/dT c'est à dire

• Conformément à la variation de volume par rapport au temps ( dV / dT )
• Inversement au carré de la distance de ce point au centre de la sphère  ( 1 / 4 pi R² )

Pour se maintenir à la même distance du centre, ce point devra s'éloigner du centre à une vitesse constante dR/dT

• Proportionnelle à la variation de volume par rapport au temps ( dV / dT )
• Inversement proportionnelle au carré de cette distance ( 1 / 4 pi R² )

Tout se passe comme si la région centrée en P   " avalait l'espace environnant "   à une vitesse constante de dV / dT

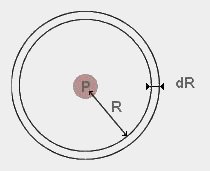
Considérons maintenant cette même sphère qui se rétrécit de façon accélérée dV / dT²   nous aurons

dV/dT² = (4 pi R² ) dR/dT²    ou bien :

dR/dT² = dV/dT² / (4 pi R² )

Pour se maintenir à la même distance du centre, ce point devra s'éloigner avec une accélération constante : dR/dT²

• Proportionnelle à la variation de la variation de volume par rapport au temps ( dV / dT²)
• Inversement proportionnelle au carré de cette distance ( 1 / 4 pi R² )

C'est exactement ce qu'une masse centrée en P produit comme effet autour d'elle, : une accélération

• Proportionnelle à la masse considérée
• Inversement proportionnelle au carré de cette distance ( 1 / 4 pi R² )

Par exemple, le nombre de m³  " avalés "  par (secondes)² par la masse de la terre serait de :

dV/dt² = 4 pi Rt². g = (surface de la terre ) . g
Avec  g = ( K Mt ) / Rt² ( accélération de la pesanteur ) donc

dV/dt² = ( 4 pi Rt²) . ( K Mt / Rt² ) = 4 pi K Mt

( dV/dt² a les même dimensions que Mt, ce qui explique que K devient une constante sans dimensions )

Par kg cela donne ( on divise par la masse de la terre Mt )
dV/dt² = 4 pi K = 8.3868 10^-10   m ³ / s ²

Avec :

• Rt = rayon de la terre
• 4 pi Rt² = surface de la terre
• Mt = masse de la terre
• g = accélération de la pesanteur sur la terre= ( K Mt ) / Rt ² = 9.81 m / s ²
• K = constante de Newton = 6.674 10^ -11

La masse pourrait donc être considérée comme la dérivée seconde du volume par rapport au temps dV / dT² comme dimension L³ / T²
1 kg = 8.3868 10^-10  m³ / s ²  ou bien  1 m³ / s ² = 1.19235 10^ 9 kg

La masse serait donc simplement une " région de l'espace " qui " avalerait " l'espace environnant de plus en plus vite. Ce point de vue correspond parfaitement à ce que nous observons d'une masse à une certaine distance : son pouvoir d'accélérer les corps vers elle

On considère souvent la masse comme une déformation locale de " l'espace-temps " pourquoi donc la masse elle-même, n'aurait pas une dimension dépendant uniquement de l'espace et du temps ?

On pourra donc définir la masse comme :

Une région de l'espace qui " avale " de plus en plus vite l'espace environnant.
L'unité naturelle de masse sera de  m³ / s²  vaudra  1 / (4 pi K )  kg  =  1.19235 10^9  kg     (1)

L'accélération a provoquée par ume masse M ( kg ) :    a = (K M / R²) en m/sec² , soit en exprimant M en m³/s²
a = ( K M / R² ) / (4 pi K)  =  (M / R²).(1/4 pi ) avec a exprimé en m/s² et M en m³/s²

Avec l'unité naturelle de masse ( m³ / s² ) et l'unité d'accélération (m / s²) la constante de Newton devient donc 1/ 4 pi

En effet l'accélération de la pesanteur g (m / s²)   =    K . Mt ( kg ) / Rt² (m²) Il faut donc diviser le second membre par 4 pi K pour avoir conformément à  (1)   des m³/s² et pas des kg,  g devient donc
g (m / s²)   =   ( 1/4 pi ) . Mt (m³/s²) / Rt² (m²)    =>    g = ( 1/4 pi ) . Mt / Rt²   en unités "naturelles"